

Molecular Mechanics: The Analysis of Steric Energy
Peter J. Hansen
This document was written for instructors. It describes a type of exercise that can provide introductory students with greater insights into the methodology of molecular mechanics.
Unlike semi-empirical and ab initio methods, molecular mechanics employs only classical physics to determine the optimum geometry of a molecule. Molecular modeling software with molecular mechanics capability (such as CAChe or PCModel) computes and displays a steric energy for an optimized structure as well as six or eight components of this steric energy. All of these components arise from essentially five phenomena:
- bond stretching,
- bond angle bending,
- bond rotation (torsion),
- van der Waals interactions, and
- electrostatic interactions.
To compute the bond stretch and bond angle contributions to the steric energy, reference values are assigned to all of a structure's bond lengths and angles, and Hooke's law is applied to the deviations from these reference values. Similarly the torsional (or dihedral) contribution arises from deviations from optimum dihedral angles (60 or 180 degrees for bonded sp3 carbons). The van der Waals term reflects (for each pair of non-bonded atoms separated by at least three bonds) the potential related to the difference between the interatomic distance and the sum of the van der Waals radii. The electrostatic term can be computed by assigning dipole moments to all bonds and computing the interactions of these dipoles using Coulomb's law.
One can usually associate features (angles, interatomic distances, and bond polarities) of an optimized structure with the values of at least five of the energy components of the structure's steric energy. For example, if bonds between sp3 carbons differ significantly from 1.523 A, the stretch term will be relatively high. (Although energy terms such as "improper torsion" or "stretch bend" (a cross term) are not amenable to this type of analysis, these terms seldom contribute significantly to the steric energy of relatively simple molecules.)
Instructors should examine conformers and geometric isomers of a variety of compounds and identify good candidates for this type of analysis. Explicit questions should be framed that require students to draw structures, perform structure optimizations, and rationalize the magnitudes of the components of the steric energy in terms of structural features.
Given below are results of the geometry optimization of 1,2-dibromoethane using CAChe software and the MM2 force field and a discussion of the major contributions to the difference in the steric energy of its gauche and anti conformers.
Example: 1,2-dibromoethane
| (energies in kcal/mol) | difference | |||
| energy term | gauche | anti | (absolute) | (% of total) |
| bond stretch | 0.074 | 0.063 | 0.011 | 0.81 |
| stretch bend | 0.076 | 0.048 | 0.028 | 2.06 |
| improp torsion | 0.000 | 0.000 | 0.000 | 0.00 |
| electrostatics | 2.135 | 1.614 | 0.521 | 38.42 |
| angle | 0.844 | 0.383 | 0.461 | 34.00 |
| dihedral | 0.122 | 0.008 | 0.114 | 8.41 |
| van der Waals | 0.999 | 0.778 | 0.221 | 16.30 |
| hydrogen bond | 0.000 | 0.000 | 0.000 | 0.00 |
| total steric energy | 4.250 | 2.894 | 1.356 | 100.0 |
Two of the eight energy terms (angle and electrostatics) account for more than two-thirds of the steric energy difference of the two conformers. Bond angle measurements revealed that two of the Br-C-H angles in the gauche conformer deviated from 109.5 degrees by 4.4 degrees -- a larger deviation by a full degree than any angle in the anti conformer.
Bromine is more electronegative than carbon, resulting in polar C-Br bonds. The gauche arrangement of the two C-Br dipoles places them nearly parallel with the like-charged ends in relative close proximity. Although the anti conformer separates the positive (carbon) ends of the dipoles by essentially the same distance, the negative (bromine) ends are separated by a much greater distance. The latter results in both reduced repulsion and electrostatic energy. Although merely qualitative, this is consistent with the relative magnitudes of the electrostatic terms for the two conformers.
Examination of non-bonded interatomic distances (together with a table of van der Waals radii), will lead to an understanding of the source of the relatively high van der Waals strain in both conformers. It is noteworthy that the Van der Waals energy term is the second largest contributor to the steric energy of each conformer, yet its contribution to the steric energy difference is only 16%.
gauche-1,2-dibromoethane
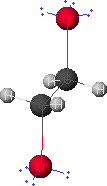
anti-1,2-dibromoethane
If you have Chime installed, click on either graphic to view graphics that you can manipulate.